一、什么是拓扑排序
在一个较为复杂的任务中,我们往往选择将其分解为数个较为简单的分任务,然后依次完成。这些分任务之间,有些具有依赖关系,必须先完成某一个才可以完成接下去的任务。类似于在学校中,为了获得学位,必须将所有课程修完。而在学习数据结构前,必须先学完某一门编程语言。或是如下,算法导论中的一个例子。
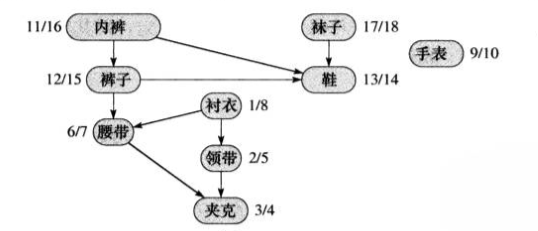
这是 Bumstead 教授每天穿衣服的次序图,必须先穿好某些衣服才能穿其他的。而教授必定是一件一件衣服穿的,那么就可以将其变为一副线性的次序图。

如上,将一副有向无环图变成线性序列的过程,称之为拓扑排序(Topological Sorting)。对于线性序列,严格的要求为:
- 每个顶点出现且只出现一次
- 如果存在一条边从 A 指向 B ,那么序列中 A 出现在 B 之前。
之所以要求是有向无环图,是因为只有有向才能在两个结点间决定先后次序。而若是有环,那么根据第二个要求,若AB间成环,则存在从 A 到 B 和从 B 到 A 两条边,那么A 要出现在 B 之前,B 也要出现在A之前,在线性序列中不可能实现。
二、实现
拓扑排序利用两种图遍历方法都可以完成。
DFS 实现
试想一下,当每次 DFS 返回的时候,对于该节点的后继必然已全部都访问完毕,那么如果在每次返回的时候输出当前结点,那么我们就可以得到一个逆拓扑序列,或者说输出的时候输出到一个列表的前端那么就是我们想要的结果。
BFS 实现
这一方法又称为 Kahn 算法,可分为如下几步:
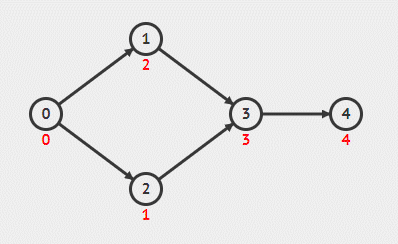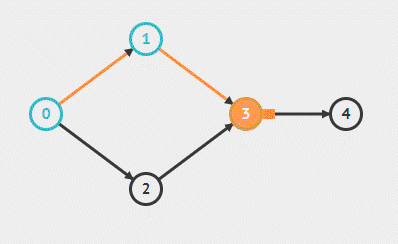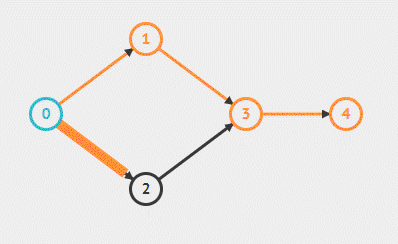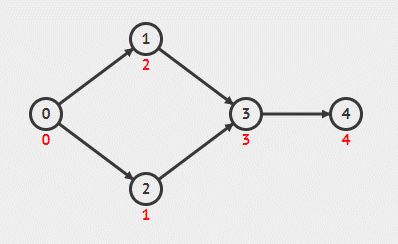
- 计算所有结点的入度,并将入度为 0 的放入一个队列
- 取出队列中第一个元素,将其输出后删除(使其相邻结点入度减一)。如果其相邻结点入度更新后为 0 ,则将其放入队列
- 重复 2 直到队列为空。如果输出数量与结点数量不符则说明图中存在环。
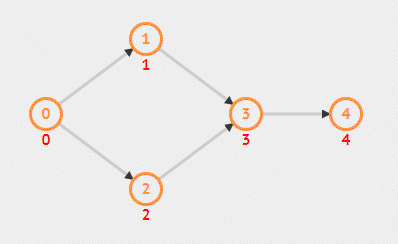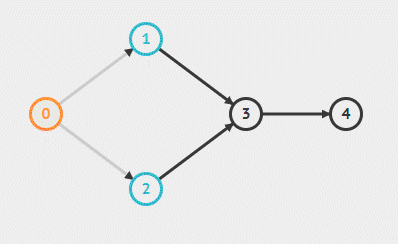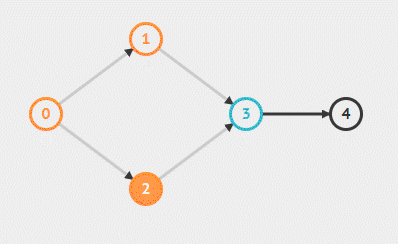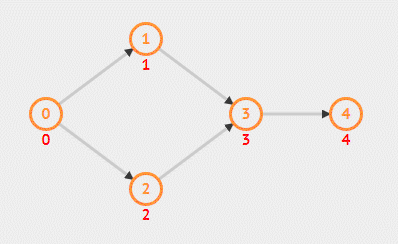
由于每次都是处理当前结点的邻接,所以是广度优先。算法之所以正确是因为,入度为 0 即代表该节点没有前驱结点,那么该结点可直接进行,那么每次只需要输出没有前驱的结点。对于邻接结点更新后入度变为 0 说明其前驱都已访问完毕,该节点可以访问了,那么可以将其输出,如此反复。
由于图算法与图本身实现有较大关联,代码并不具有通用性,所以这里给出Java实现的链接供参考。
图自算法导论
Gif 根据visugo.net 制作