基本概念
图(Graph)是一种表示物件和物件之间关系的方法,是图论的基本研究对象,由顶点(Vertex)和边(Edge)组成。
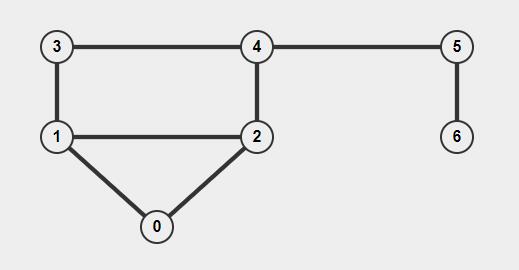
如图所示即为一个最基本的图,小圆点即为顶点,连接顶点的线即为边。通常以 \(\vert V \vert\) 来表示顶点数量,\(\vert E \vert\) 代表边的数量。当两个顶点中存在直接相连的边则称这两个点邻接(adjacent)。
图有如下几种类别。
| 类别 | 定义 |
|---|---|
| 有向图 | 图中每一条边都被规定一个方向,则为有向图,边被称为有向边。 |
| 无向图 | 与有向图相反,如果边没有规定方向则为无向图。 |
| 简单图 | 图中每两个顶点(有向图则是每个方向)最多只有一条边,并且顶点不连向自己。 |
| 多重图 | 允许图中两个顶点间有多于一条的边,而且边可以连接同一个顶点。 |
| 基础图 | 对于一个有向图,去除其边上方向的图则为该有向图的基础图。 |
| 连通图 | 如果一个无向图中,每个点到其他每一个点有一条路径,则为连通的(connected)。 |
| 强连通图 | 对于有向图,若满足连通图性质则为强连通的(strongly connected)。 |
| 弱连通图 | 对于不是强连通的有向图,如果其基础图(Underlying Graph)为连通的,则为弱连通(weakly connected)。 |
| 完全图 | 每两个结点之间如果都存在一条边则称为完全图(Complete Graph)。 |
邻接矩阵
邻接矩阵(Adjacency Matrix)是一个大小为 \(\vert V \vert \vert V \vert\) 的二维数组。将顶点进行编号,从 0 到 n ,则对于 \(Adj[i][j]\) ,则代表第 i 个顶点到第 j 个顶点的边。对于无权重的图,值为 0 代表不存在这条路,1 则代表存在这条路。对于有权重的图,则可以用具体权重大小来代替无权重图中的 1 。
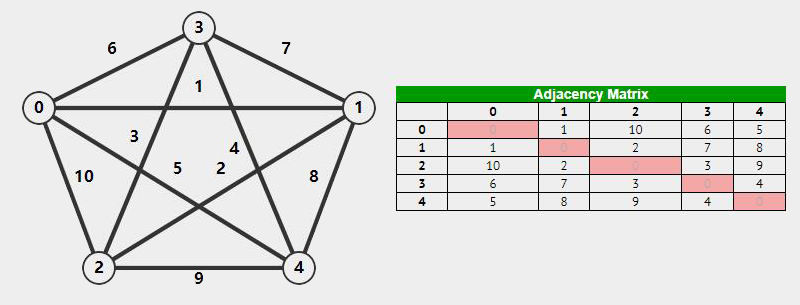
对于无向图而言,邻接链表表示法可以只要求一半的存储空间,因为对于无向图的邻接矩阵而言,其转置即为其本身。
邻接链表
邻接链表(Adjacency List)由 \(\vert V \vert\) 个链表组成,每一个表头为一个顶点,链表中每个节点则为与表头顶点相连的顶点,并同时记录着边权重大小。
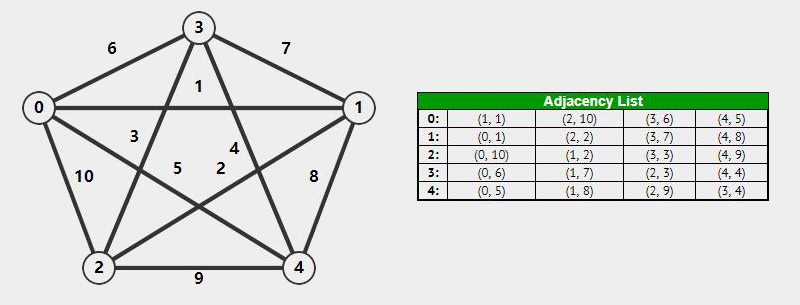
比较
两种表示方法都可以很好的表示一张图,但是邻接链表无法快速给出两个顶点间边的性质,相对而言邻接矩阵很好的克服了这一问题,但同时付出了更大的存储空间作为代价。 所以一般而言,在图的规模较小的情况下,更倾向于用邻接矩阵的方式来表示。
图片和gif根据 visualgo.net 制作